- Index
- index
- README
- Sommaire Informatique
- Sommaire Maths
- Sommaire Chimie
- Sommaire Physiques
- Régime transitoire
- Nombres complexes
- Formules de Taylor
- Espace vectoriel
- Séries numériques
- Loi de composition
- variables et opérations
- Régime pseudo-périodique
- Bases locales
- Matrices
- Probabilités
- Suites numériques
- Comparaisons locale de fonctions
- Relation binaire
- Intégration
- Continuité
- Sommes et produits
- Nombres quantiques
- Ensembles
- Théorème des gendarmes
- Ondes acoustiques
- Champs de vecteurs
- Ecriture complexe et Impédances
- Intégration discrète
- Valeur propre
- Lambda-Calcul
- Fonctions hyperboliques
- Pivot de Gauss
- Dérivée
- Calcul Polynomial
- Binôme de newton
- Configuration Atomique
- Logique
- Nabla
- Fonctions de la variable réelle
- Déterminants
- Laplacien
- lancer un programme
- Série de Reimann
- Ondes mécaniques
- Schéma de Thévenin-Norton
- Divergence
- Fonctions trigonométriques
- Gradient
- Développements généralisés
- Développements limités
- Systèmes de coordonnées
- Reduction d'endomorphisme
- Méthode Acide-Bases
- Nomenclature
- Raisonnements logiques
- Structure de groupes
- Intervalle et voisinage
- Théorème des accroissements finis
- Applications linéaires
- Régime apériodique
- Energie d'ionisation
- Analyse Vectorielle
- Constante d'équilibre
- Equations différentielles linéaires
- Systèmes linéaires
- Fractions rationnelles
- Décomposition en éléments simples
- Puissance Electrique
- Oscillateur Harmonique
- Polynomes
- Preuve GL est un groupe
Suites numériques
algebra
Une suite est une application de \(\mathbb{N}\) vers \(\mathbb{R}\). Soit \(u\) une telle application, on note son image par \(n\), \(u_n\) appelé \(n\)-ieme terme de la suite \((u_n)_{n\in \mathbb{R}}\). Soit une suite \((u_n)_{n \in \mathbb{N}}\), on considère son image comme une partie des réels. On dit que la suite est minorée, majorée ou bornée si son image l'est.
De plus, elle reste une application, donc les règles de croissance sont applicables.
Les suites sont stables par combinaisons linéaires. On défini aussi le produit de suites comme le produits de leurs termes. (ex. \(\forall n \in \mathbb{N},\quad (u \times v)_n = u_n \times v_n\))
Limites
On ne considère la limite d'une suite que vers \(+ \infty\). On a alors deux cas :- (\(u_n\)) converge vers \(\mathcal{l}\) si
- (\(u_n\)) diverge vers \(+ \infty\) (resp. \(- \infty\)) si
On considère \(\mathcal{E}\) une "précision", et on dit qu'il existe \(n_0\) tel que a partir de \(n_0\), tous les termes de la suites sont a \(\mathcal{E}\) pres d'un réel \(\mathcal{l}\).
Si une suite converge, sa limite est unique. On a aussi que toute suite convergente est bornée, mais pas l'inverse.
Si deux suites sont convergentes, alors leurs limites sont stables par toutes les operations classiques, ainsi que par produit.
Suites adjacentes
Deux suites sont dit adjacentes si:1. L'une est croissante et l'autre est décroissantes
2. (\(u_n - v_n\)) \(\rightarrow\) 0
Deux suites adjacentes ont donc la meme limite.
Suites extraites
On appel suite extraite une suite \(v_n\) tel que :\[ v_n = u_{f(n)} \]
avec \(f(n)\) une fonction extractrice. On a donc \(Im(f) \subset \mathbb{N}\).
Si une suite \(u_n\) converge vers \(l\), toutes les suites extraites convergent vers \(l\).
De toute suite bornée on peut extraire une suite convergente.
Pour prouver qu'une suite est divergente il suffit donc de trouver deux suites extraites qui convergent vers des limites différentes.
Suite récurrentes
On appel une suite récurrente une suite définie par elle meme. Par exemple :\[ u_{n+1} = f(u_n) \]
On a alors quelques cas particuliers :
- Si \(f\) est de la forme \(x \to x+r\), \(u_n\) est une suite arithmétique
- Si \(f\) est de la forme \(x \to \lambda x\) , \(u_n\) est une suite géométrique
- Si \(f\) est de la forme \(x \to \lambda x+r\), \(u_n\) est une suite arithmético-géométrique
- si \(f\) est croissante, \(u_n\) est monotone
- si \(f\) est décroissante, \(u_{2n}\) et \(u_{2n+1}\) sont monotones de sens contraires.
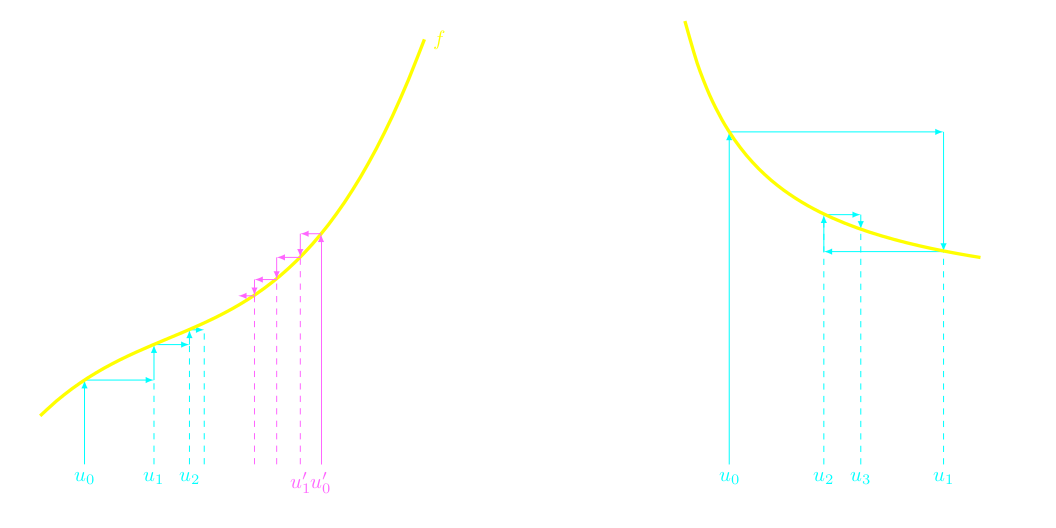
On as alors que, si \(u_n\) est convergente, sa limite \(l\) est un point fixe, c'est a dire :
\[ f(l) = l \]
La forme \(u_{n+1} = f(u_n)\) est une suite récurrente d'ordre 1. On peut aussi considérer des suites récurrentes de la forme \(u_{n+2} = au_{n+1} + bu_n\). Une expression de la forme peut être convertie en suite "classique" de la manière suivante :
- On étudie l'équation caractéristique \(r^2 = ar + b\)
- Si \(r\) admets deux solutions distinctes :
- Si \(r\) admets une racine double : \(u_n = (\lambda + \mu n)r^n, \quad (\lambda, \mu) \in \mathbb{R}^2\)
- Si \(r\) admet des racines complexes conjuguées de la forme \(re^{ia}, re^{-ia}\) \(u_n = r^n(\lambda cos(na) + \mu sin(na))\)
Cette méthode de résolution est proche de celle des equations différentielles.